◌◌◌ Line
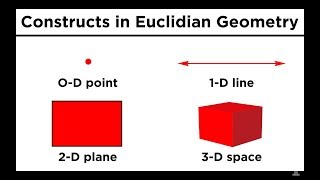
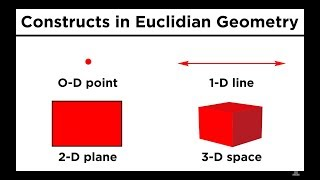
From here, we can construct a one-
dimensional object by stringing an infinite number of points along a particular
dimension. This object is called a line.
http://qindex.info/i.php?x=5177
◌◌◌ Space
By stringing an infinite number of lines along a
dimension perpendicular to the line, a two-
dimensional object called a plane can be obtained. And then if we string an infinite number of planes in either direction, we get three
dimensional space.
http://qindex.info/i.php?x=5178
• Cross Product
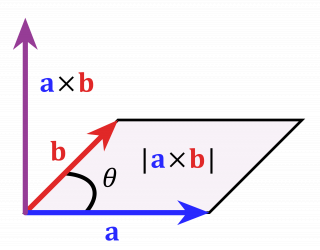
Given two nonzero vectors in two or three
dimensions, their cross product is a vector with magnitude equal to the product of the magnitudes of the vectors times the sine of the angle between the vectors and direction perpendicular to the vectors.
http://qindex.info/i.php?x=5291
◌◌◌ Plane
By stringing an infinite number of lines along a
dimension perpendicular to the line, a two-
dimensional object called a plane can be obtained. And then if we string an infinite number of planes in either direction, we get three
dimensional space.
http://qindex.info/i.php?x=5031
• Leonard Susskind
The space itself may be more than three
dimensions. But we can't visualize more
dimensions. The architecture of the brain itself is evolved in the world of three
dimensions. We only describe more
dimensions by pure mathematics.
http://qindex.info/i.php?x=5242
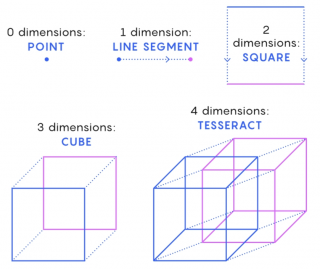• dimension ⪢⪢
○○○ Point ⪢⪢
• dimension
• What are quaternions, and how do you visualize them? A story of four dimensions.
• Thinking visually about higher dimensions
• dimension
