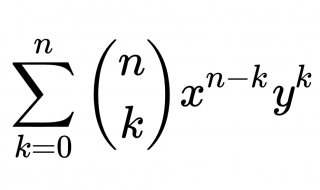• 322_ Binomial Expansion
ᐥ(a+b)˄n = ｢｢nꞒk｣·a˄(n−k)·b˄k Σk=0,n｣ = ｢n!/((n−k)!·k!)·a˄(n−k)·b˄k Σk=0,n｣ᐥ (a+b)˄1 = ｢1!/((1−k)!·k!)·a˄(1−k)·b˄k Σk=0,1｣ = a+b (a+b)˄2 = ｢2!/((2−k)!·k!)·a˄(2−k)·b˄k Σk=0,2｣ = a˄2+2·a·b+b˄2 (a+b)˄(n+1) = (a+b)˄n·(a+b) = (a+b)˄n·a+(a+b)˄n·b = ｢n!/((n−k ...
http://qindex.info/i.php?x=9688