Glome, Hollow Glome and Luffa
 •
3-sphere
•
3-sphere
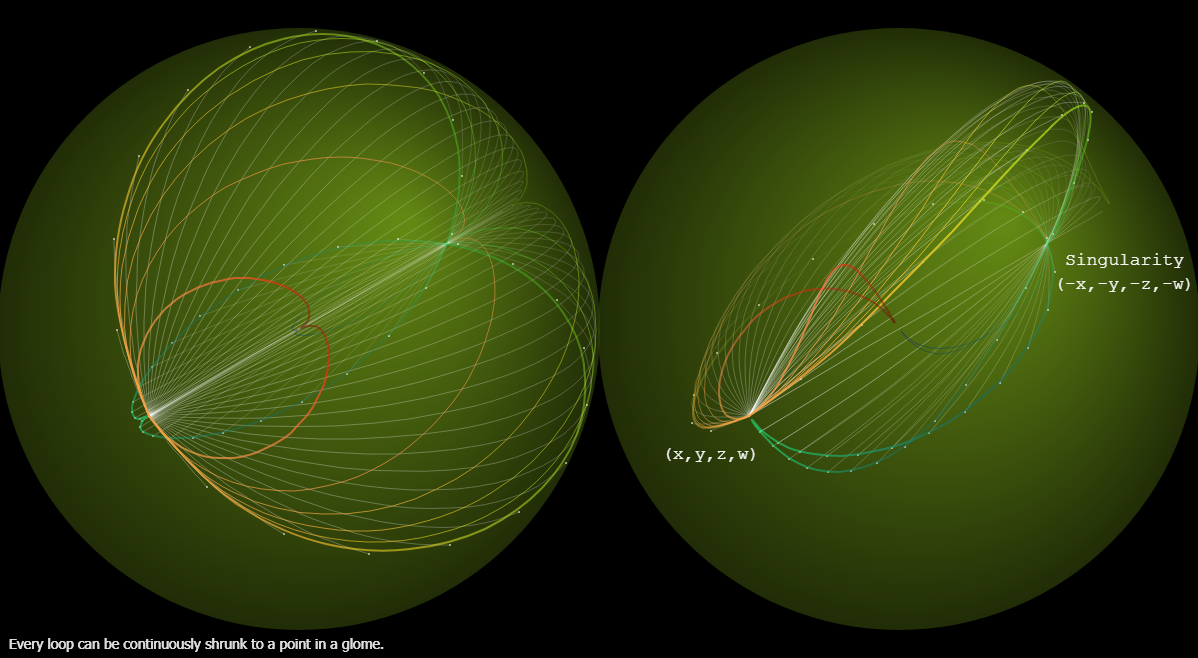
Any loop or circular path on the 3-sphere can be continuously shrunk to a point without leaving the 3-sphere. The Poincaré conjecture provides that the 3-sphere is the only three-dimensional manifold (up to homeomorphism) with these properties.
5253#3447
SIBLINGS
CHILDREN
3447
•
Compact space
Compactness is a property that generalizes the notion of a subset of Euclidean space being closed (that is, containing all its limit points) and bounded(that is, having all its points lie within some fixed distance of each other).
5253#3494
SIBLINGS
CHILDREN
3494
•
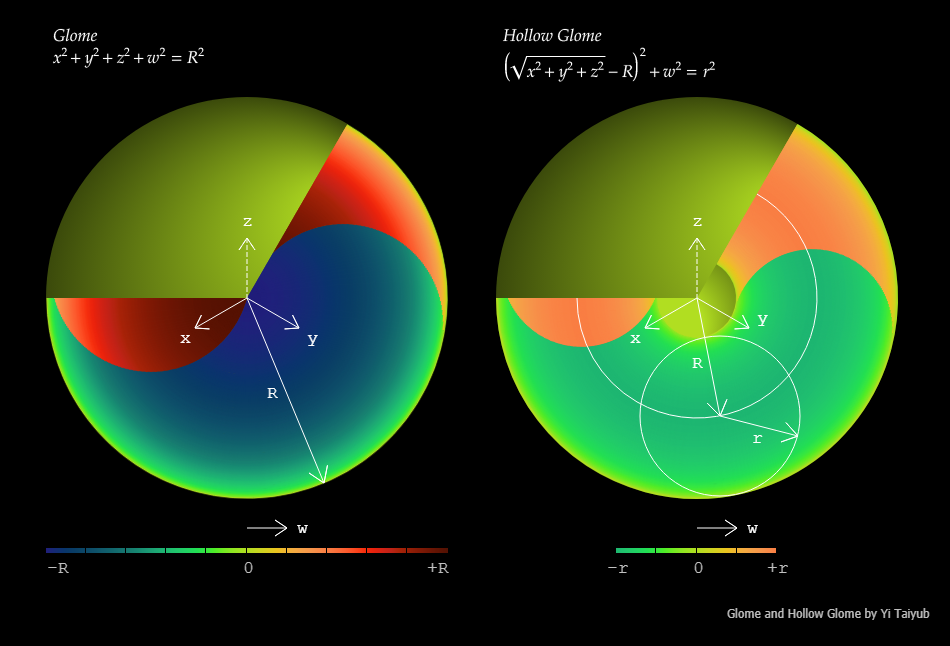
Glome in colors 01
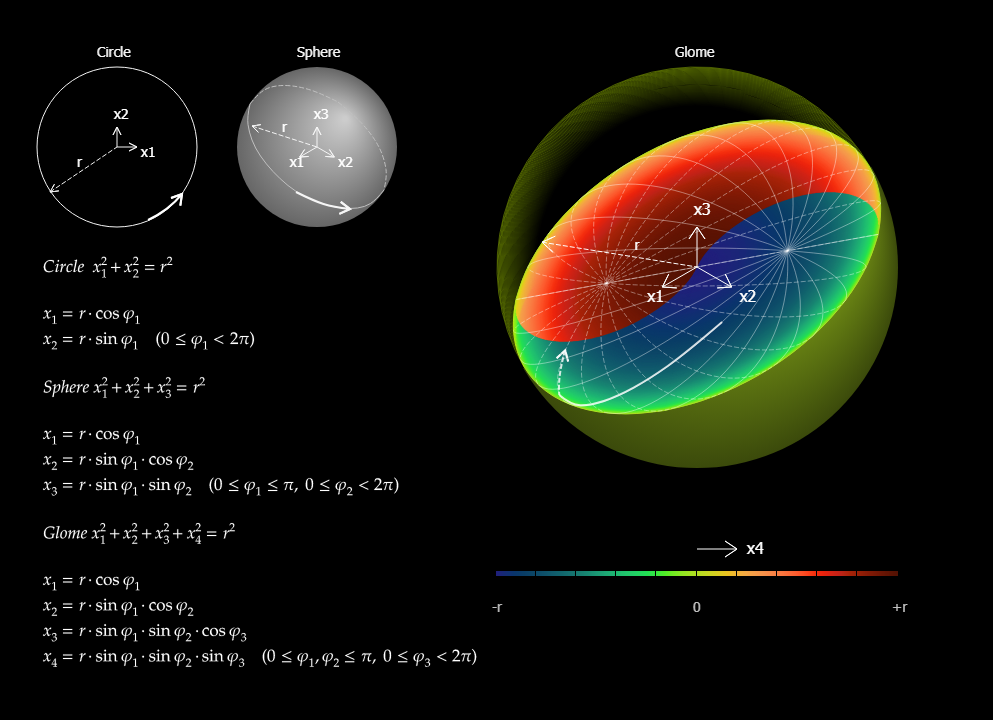
What is the shape of the universe?
Does it extend infinitely?
We can go around the earth forever but can not find the end. Likewise, the universe may be finite but endless.
Let's consider a mathematical model suitable for such a space.
A summary of Eucli ...
5253#707
SIBLINGS
CHILDREN
COMMENT
707
•
Glome in colors 03
In a one-dimensional space, there is only one direction. So it is straight. If a one-dimensional space is looped, the relationship between points can be represented by a closed curve. But the curve shows just the relationship between points, not the shape ...
5253#9044
SIBLINGS
CHILDREN
COMMENT
9044
•
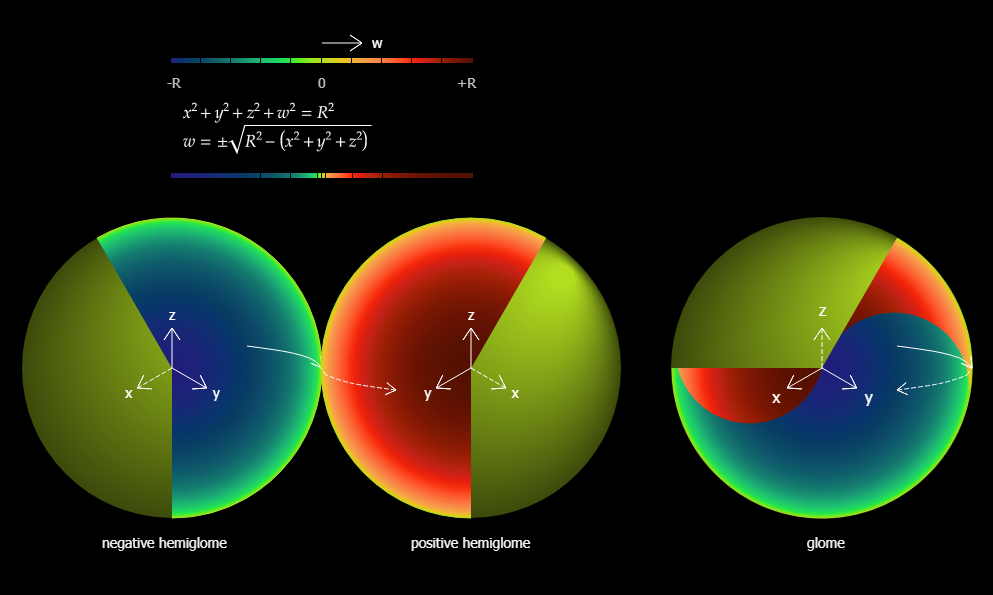
Glome in colors 04
All paths are reflected at the boundary of the glome making the space bounded without a boundary. Every path passing through any point in the glome is continuous at the point even at the boundary.
This is analogous to the projection of a sphere.
5253#9045
SIBLINGS
CHILDREN
COMMENT
9045
•
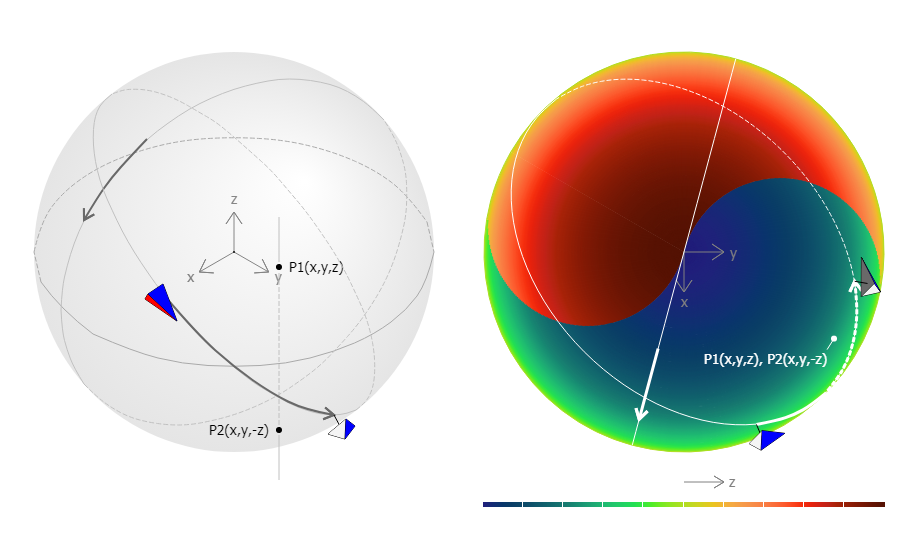
Glome in colors 06
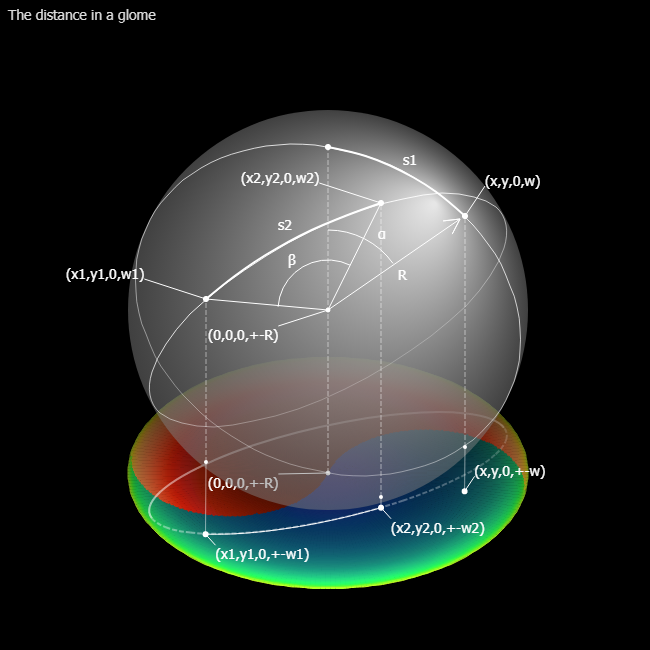
In the projection of a sphere, each point on the disc except the circumference represents two points. One is a point on the upper hemisphere and the other is a point on the lower hemisphere. Likewise, each point in the glome except the surface represents ...
5253#9048
SIBLINGS
CHILDREN
COMMENT
9048

•
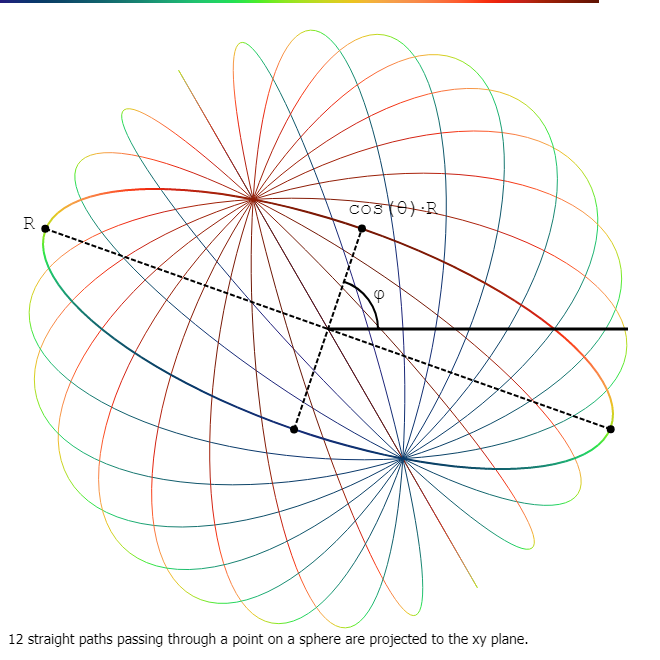
Glome in colors 10
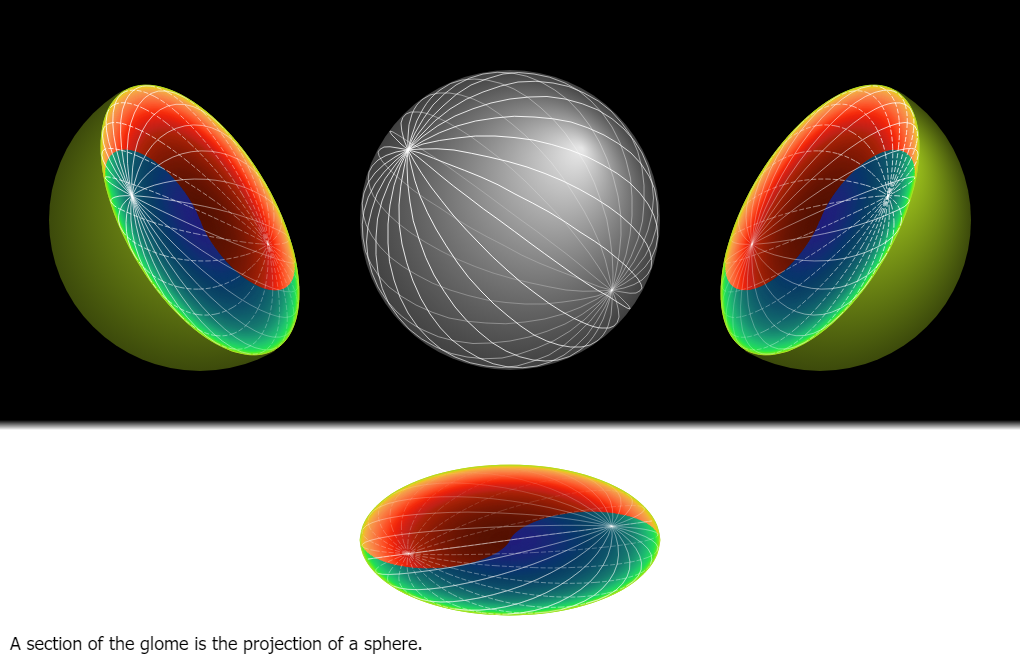
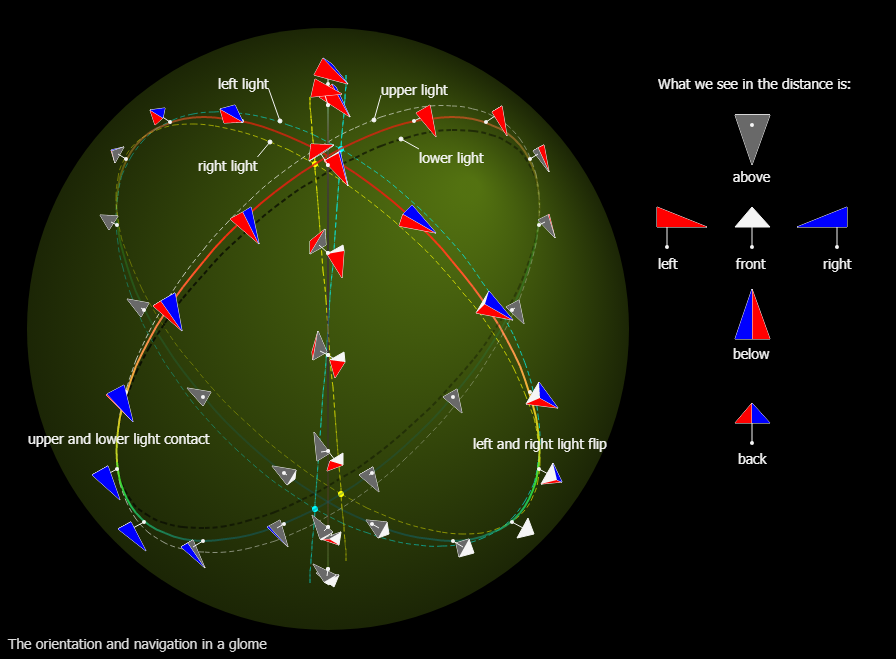
Going straight is represented by following an ellipse on the great section and the movement from one hemiglome to another is represented by the contact between the ellipse and the circumference of the great section.
For every direction at any point in a g ...
5253#9052
SIBLINGS
CHILDREN
COMMENT
9052

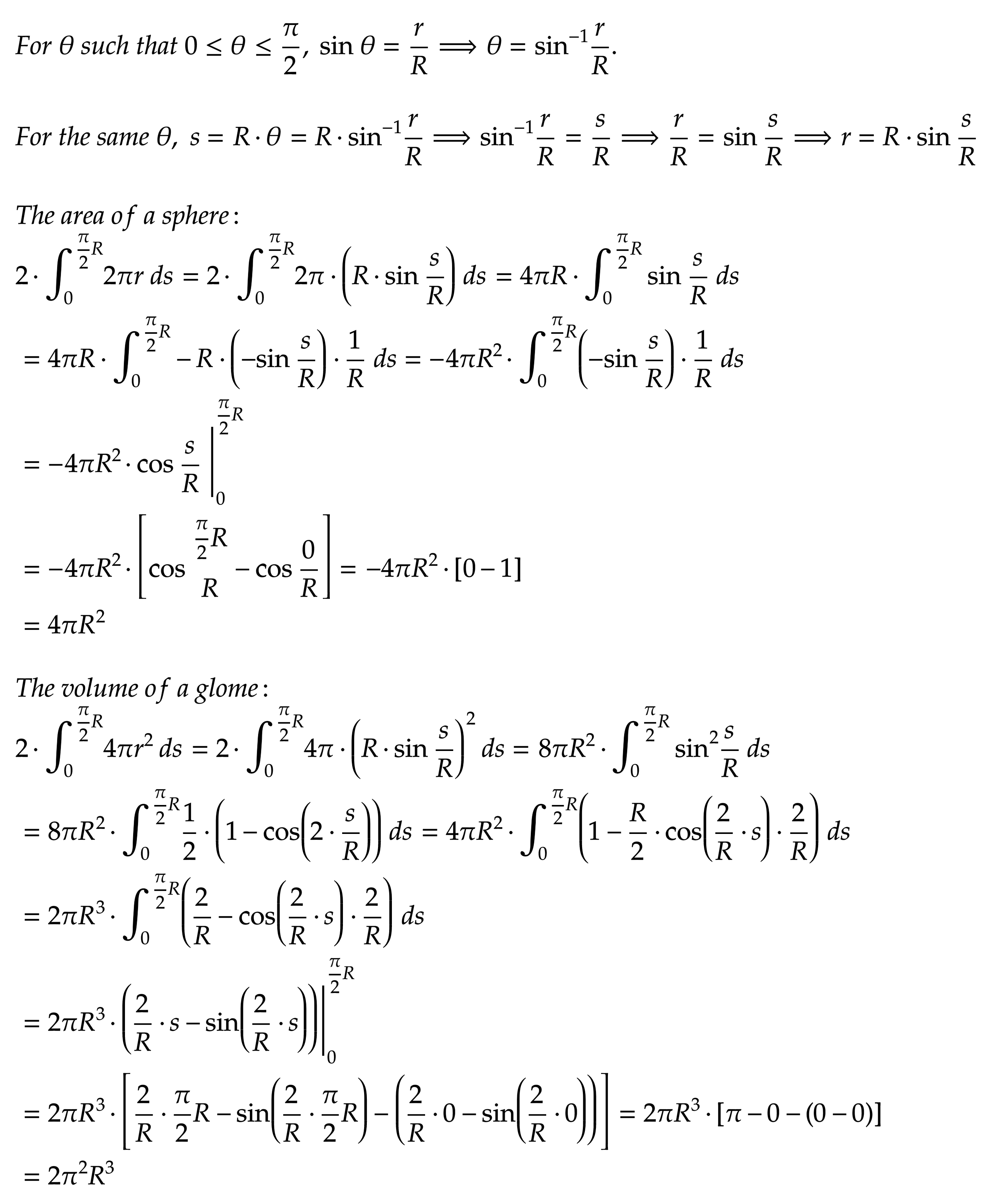
•
Glome in colors 15
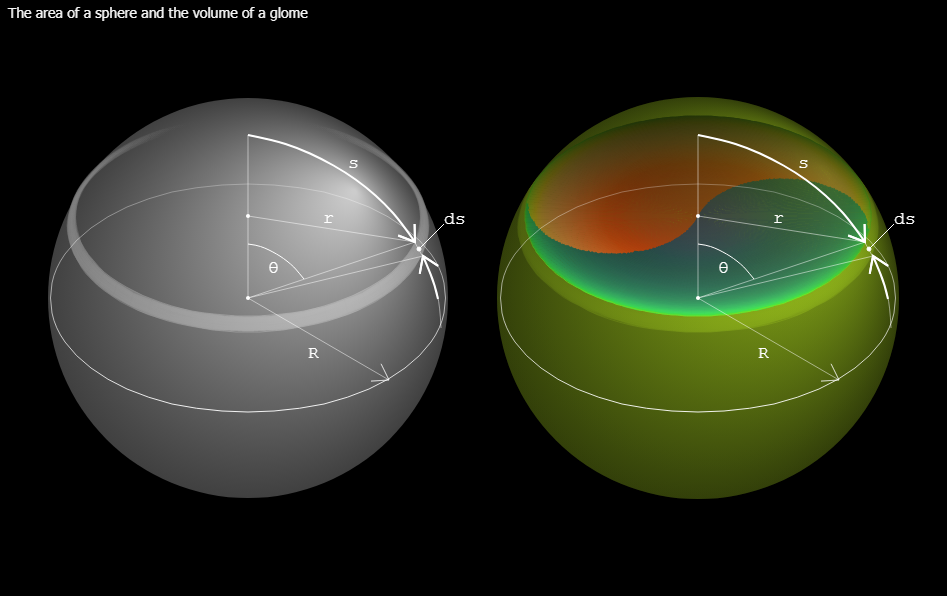
A circular model has two dimensions, but the space represented by the model has only one dimension. The spheric model has three dimensions, but there are only two dimensions in the space that the model represents. Likewise, the space represented by the gl ...
5253#9058
SIBLINGS
CHILDREN
COMMENT
9058

•
Glome in colors 18
For any two points in a glome, there is a plane containing the two points and the origin. By cutting the glome with the plane we get a great section where we can draw a great ellipse passing through the two points. This means that at any point in a glome ...
5253#9061
SIBLINGS
CHILDREN
COMMENT
9061



•
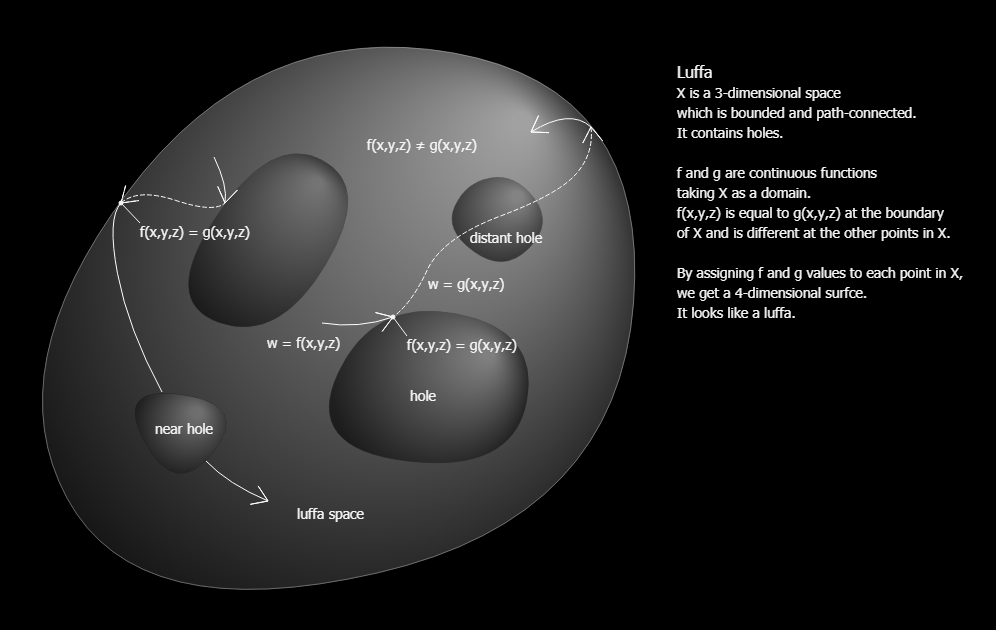
Hollow Glome and Luffa 06
Suppose a three-dimensional space which is bounded and path-connected. Let the space contain holes.
Let f and g be continuous functions taking this space as a domain.
f(x,y,z) is equal to g(x,y,z) at the boundary of the space and is different at the other ...
5253#9069
SIBLINGS
CHILDREN
COMMENT
9069
 •
Leonard Susskind
•
Leonard Susskind
The space itself may be more than three dimensions. But we can't visualize more dimensions. The architecture of the brain itself is evolved in the world of three dimensions. We only describe more dimensions by pure mathematics.
5253#5242
SIBLINGS
CHILDREN
5242
 •
n-sphere
•
n-sphere
A set of points at a specified distance from a particular point in (n+1)-dimensional space.
The pair of points at the ends of a line segment is a 0-sphere.
5253#3446
SIBLINGS
CHILDREN
3446
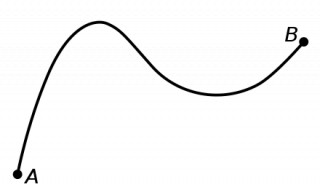 ◌◌◌
Path
◌◌◌
Path
In mathematics, a path in a topological space X is a continuous function f from the unit interval I = [0,1] to X
f : I → X.
A topological space for which there exists a path connecting any two points is said to be path-connected.
5253#3453
SIBLINGS
CHILDREN
3453
•
Real coordinate space
In mathematics, real coordinate space of n dimensions, written Rn (/ɑːrˈɛn/ ar-EN) (also written ℝn with blackboard bold) is a coordinate space that allows several (n) real variables to be treated as a single variable.
5253#3495
SIBLINGS
CHILDREN
3495
•
Simply connected space
A sphere (or, equivalently, a rubber ball with a hollow center) is simply connected, because any loop on the surface of a sphere can contract to a point, even though it has a "hole" in the hollow center.
5253#3577
SIBLINGS
CHILDREN
3577
 •
The Poincare Conjecture
•
The Poincare Conjecture
In the early 1900s mathematicians and physicists were very interested in the shape of space. New experiments and theories were being developed that would ultimately create relativity theory and change our entire view of the universe.
5253#3533
SIBLINGS
CHILDREN
3533
•
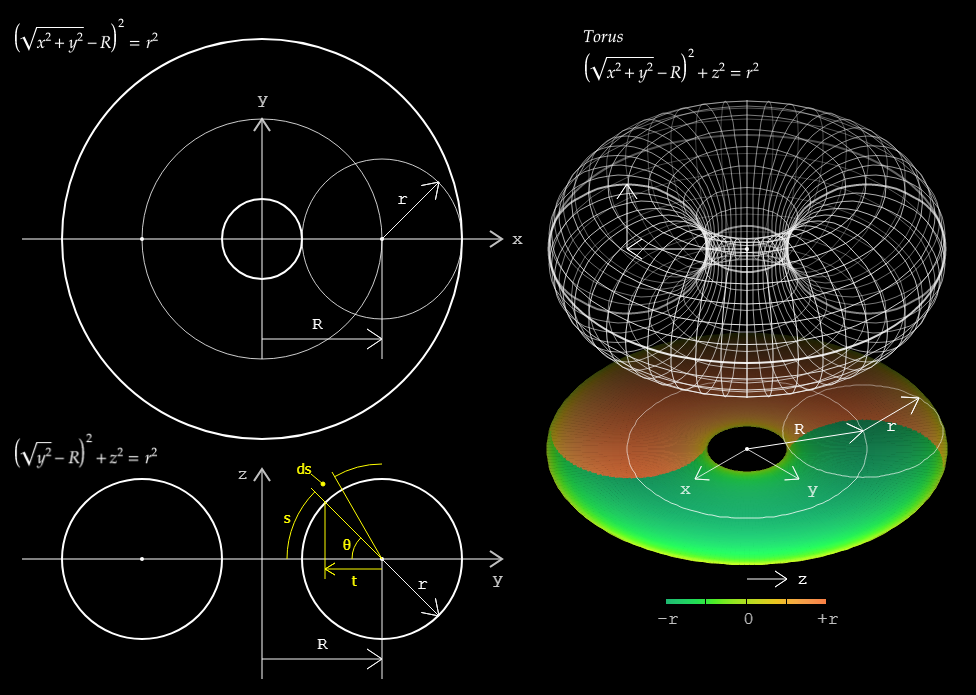
Three-torus
The three-dimensional torus, or triple torus, is defined as the Cartesian product of three circles. The triple torus is a three-dimensional compact manifold with no boundary.
5253#3612
SIBLINGS
CHILDREN
3612

-

 •
3-sphere
•
3-sphere









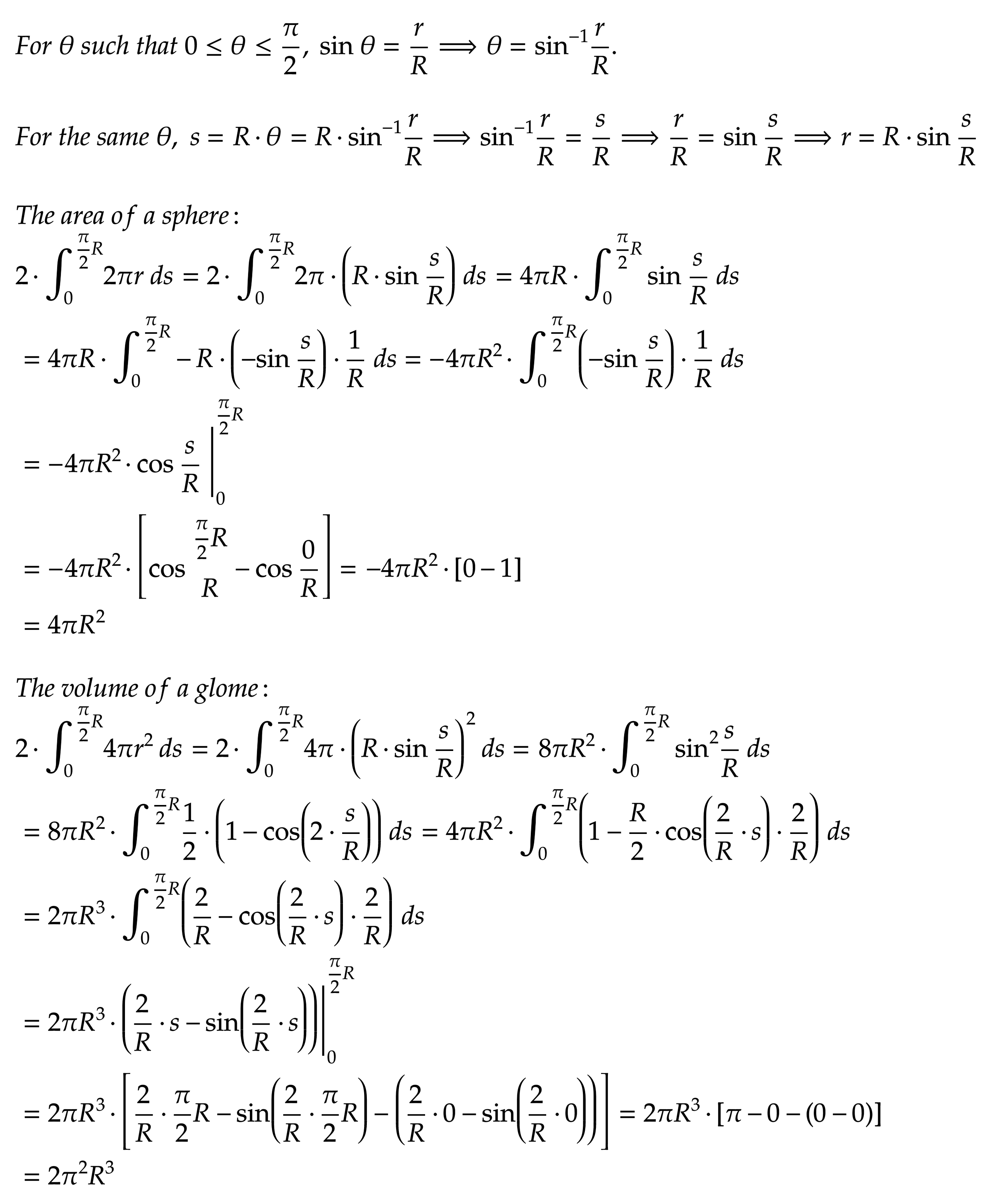










 •
Leonard Susskind
•
Leonard Susskind
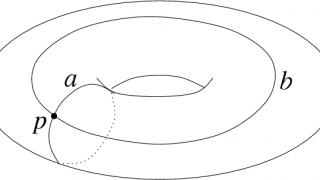 ◌◌◌
Loop
◌◌◌
Loop
 •
n-ball
•
n-ball
 •
n-sphere
•
n-sphere
 ◌◌◌
Path
◌◌◌
Path
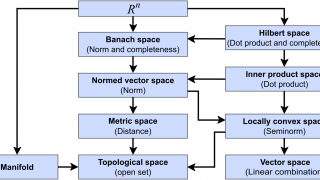 ◌◌◌
Space
◌◌◌
Space
 •
The Poincare Conjecture
•
The Poincare Conjecture
 •
Thinking visually about higher dimensions
•
Thinking visually about higher dimensions
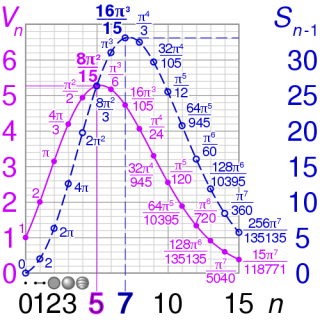 •
volumes and surface areas of n-spheres
•
volumes and surface areas of n-spheres