 •
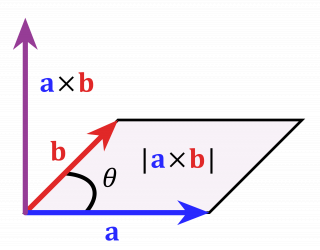
Cross Product
•
Cross Product
Given two nonzero vectors in two or three dimensions, their cross product is a vector with magnitude equal to the product of the magnitudes of the vectors times the sine of the angle between the vectors and direction perpendicular to the vectors.
5079#5291
SIBLINGS
CHILDREN
5291
 ◌◌◌
Line
◌◌◌
Line
From here, we can construct a one- dimensional object by stringing an infinite number of points along a particular dimension. This object is called a line.
5079#5177
SIBLINGS
CHILDREN
5177
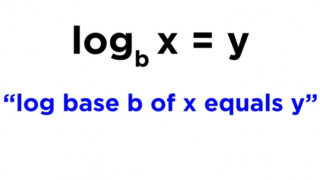 ○○○
logarithm ⪢⪢
○○○
logarithm ⪢⪢
With logs, the base of the log raised to the power of what's on the other side of the equal sign will equal the number that the log is operating on. ┆ x⍻b = y ➔ b˄y = x
#math
5079#28240
SIBLINGS
CHILDREN
28240
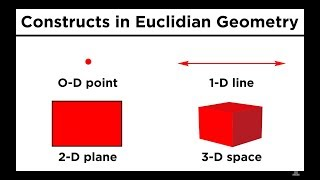 ◌◌◌
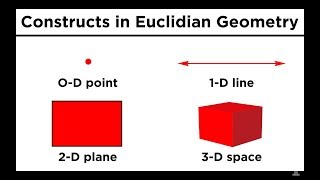
Plane
◌◌◌
Plane
By stringing an infinite number of lines along a dimension perpendicular to the line, a two-dimensional object called a plane can be obtained. And then if we string an infinite number of planes in either direction, we get three dimensional space.
5079#5031
SIBLINGS
CHILDREN
5031
 ○○○
Point ⪢⪢
○○○
Point ⪢⪢
First we look at a point. This is nothing more than a location in space. It is zero-dimensional, meaning that it has no dimensions of any kind. #math
5079#5030
SIBLINGS
CHILDREN
5030
 ◌◌◌
Space
◌◌◌
Space
By stringing an infinite number of lines along a dimension perpendicular to the line, a two-dimensional object called a plane can be obtained. And then if we string an infinite number of planes in either direction, we get three dimensional space.
5079#5178
SIBLINGS
CHILDREN
5178
 ○○○
Φ ≈ 1.618 ⪢⪢
○○○
Φ ≈ 1.618 ⪢⪢
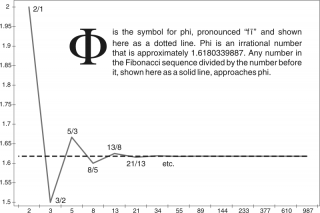
Keplar observed that the relationship between a number in the Fibonacci sequence and the previous number more and more closely approaches the irrational number Φ, the longer the sequence is continued. #math #bookmark
5079#9464
SIBLINGS
CHILDREN
9464
 •
√2 ≈ 1.414
•
√2 ≈ 1.414
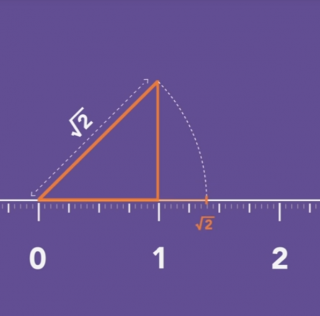
According to Pythagoras theorem the diagonal length of a square with each side measuring one unit would be square root of two.
The assumption that square root of two could be expressed as a ratio of two integers deduces a contradiction. #math
5079#9592
SIBLINGS
CHILDREN
9592

-

 ◎◎◎
complement ⪢⪢
◎◎◎
complement ⪢⪢
 ◎◎◎
complementary ⪢⪢
◎◎◎
complementary ⪢⪢
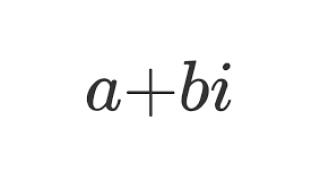 ○○○
complex number ⪢⪢
○○○
complex number ⪢⪢
 •
Cross Product
•
Cross Product
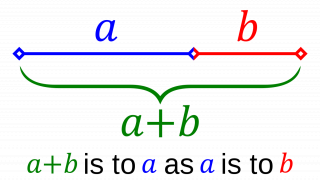 ○○○
Golden Section ⪢⪢
○○○
Golden Section ⪢⪢
 •
Greek alphabet
•
Greek alphabet
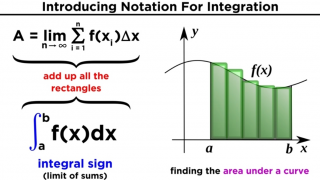 ◌◌◌
Integration
◌◌◌
Integration
 •
irrational number
•
irrational number
 ◌◌◌
Line
◌◌◌
Line
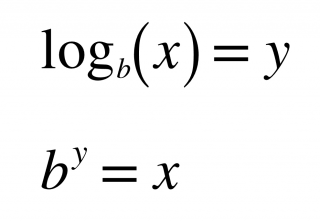 ○○○
logarithm ⪢⪢
○○○
logarithm ⪢⪢
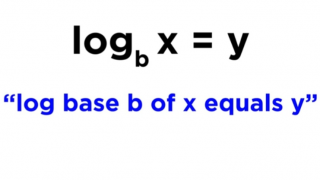 ○○○
logarithm ⪢⪢
○○○
logarithm ⪢⪢
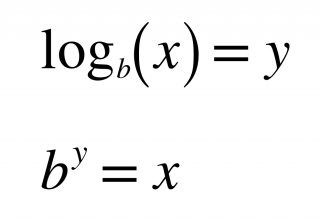 ○○○
logarithm ⪢⪢
○○○
logarithm ⪢⪢
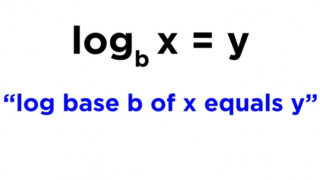 ○○○
logarithm ⪢⪢
○○○
logarithm ⪢⪢
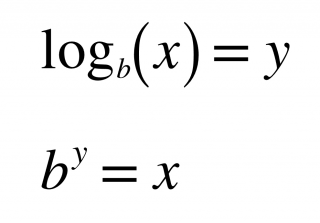 ○○○
logarithm ⪢⪢
○○○
logarithm ⪢⪢
 •
Mathematical Induction
•
Mathematical Induction
 ◌◌◌
Plane
◌◌◌
Plane
 ○○○
Point ⪢⪢
○○○
Point ⪢⪢
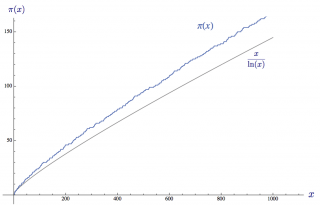 •
prime number theorem
•
prime number theorem
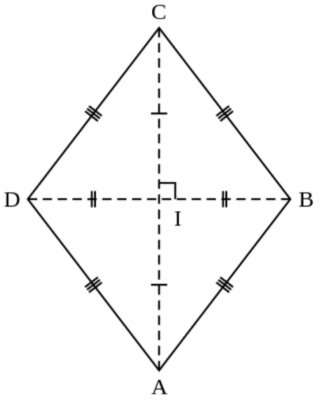 ○○○
rhombus ⪢⪢
○○○
rhombus ⪢⪢
 ◌◌◌
Space
◌◌◌
Space
 ○○○
Φ ≈ 1.618 ⪢⪢
○○○
Φ ≈ 1.618 ⪢⪢
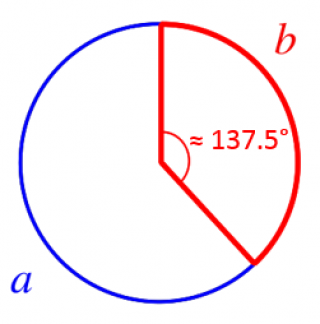 ○○○
ψ ≈ 137.5° ⪢⪢
○○○
ψ ≈ 137.5° ⪢⪢
 •
√2 ≈ 1.414
•
√2 ≈ 1.414