211 √2

• 21 Expansion of Numbers and Operations
ᐥoperators + − ×(·) / ˄ ˅ ⍻ numbers ℕ ℤ ℚ ℝᐥ The whole numbers are closed under addition. Subtraction is the inverse operation of addition. l + m = n n - m = l Define negative integers then integers are closed under subtraction. Multiplication is repea ...
9705#9540 SIBLINGS CHILDREN COMMENT 9540

• 21 Fundamental theorem of arithmetic
Every natural number either is a prime number itself or can be represented as the product of prime numbers and this representation is unique, except for the order of the factors. (unique factorization theorem, unique prime factorization theorem)
9705#9706 SIBLINGS CHILDREN 9706

• 21 Rational number
A number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q.
9705#9708 SIBLINGS CHILDREN 9708

• 211 Decimal
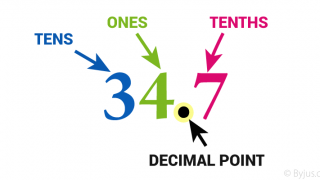
The decimal numeral system (base-ten positional numeral system, denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system.
9705#9712 SIBLINGS CHILDREN 9712

• 211 Decimal expansion
The decimal expansion of any rational number is either a terminating or a recurring decimal.
9705#9715 SIBLINGS CHILDREN 9715

• 211 √2
There is no rational number whose square is 2.
9705#9710 SIBLINGS CHILDREN 9710

Songs in Easy English

• 212 a+b√2(a,b∈ℚ) ∉ ℚ
If m/n and p/q are rationals, p≠0, then m/n+√2(p/q) is irrational.
9705#9709 SIBLINGS CHILDREN 9709

• 213 ∀a,b∈ℚ and a≠b, ∃c in (a,b) and c∉ℚ
Between any two distinct rationals there is an irrational.
9705#9711 SIBLINGS CHILDREN 9711

• 223
The density of Q and other consequences of the Axiom of Completeness.
9705#9761 SIBLINGS CHILDREN 9761

• 223 Completeness Axiom
ᐥEvery non-empty set of real numbers that is bounded above has a least upper bound. Every non-empty set of real numbers that is bounded below has a greatest lower bound.ᐥ
9705#9746 SIBLINGS CHILDREN 9746

• 223 Infimum and supremum
9705#9748 SIBLINGS CHILDREN 9748

• 223 The Supremum and Completeness of ℝ
9705#9760 SIBLINGS CHILDREN 9760

• 233 Mathematical Induction
9705#9717 SIBLINGS CHILDREN 9717

• 233 Mathematical Induction
Let P(n) be a statement for each natural number n. If (a) P(1) is true, and (b) P(k) true ⇒ P(k+1) true for every natural number k∈ℕ then P(n) is true for all n∈ℕ.
9705#9749 SIBLINGS CHILDREN 9749