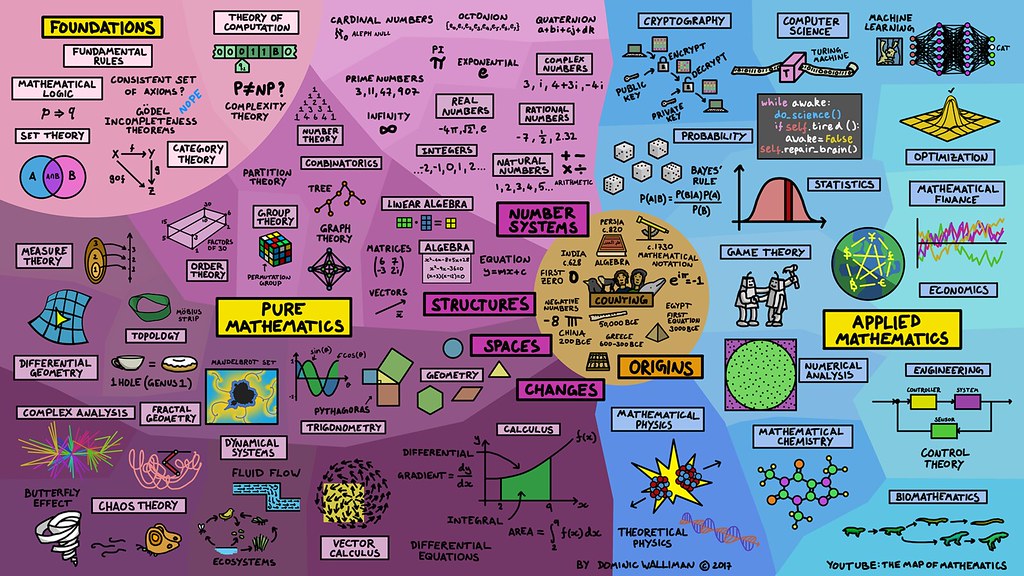
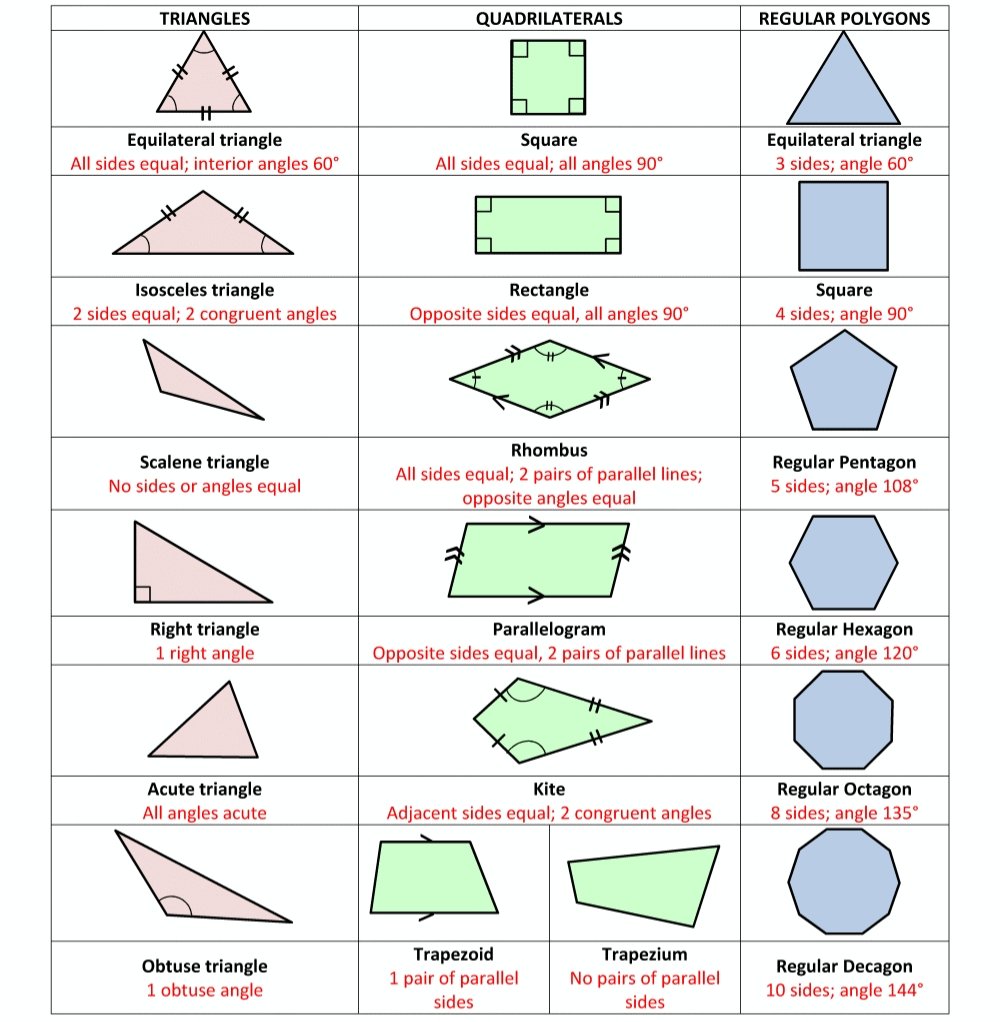
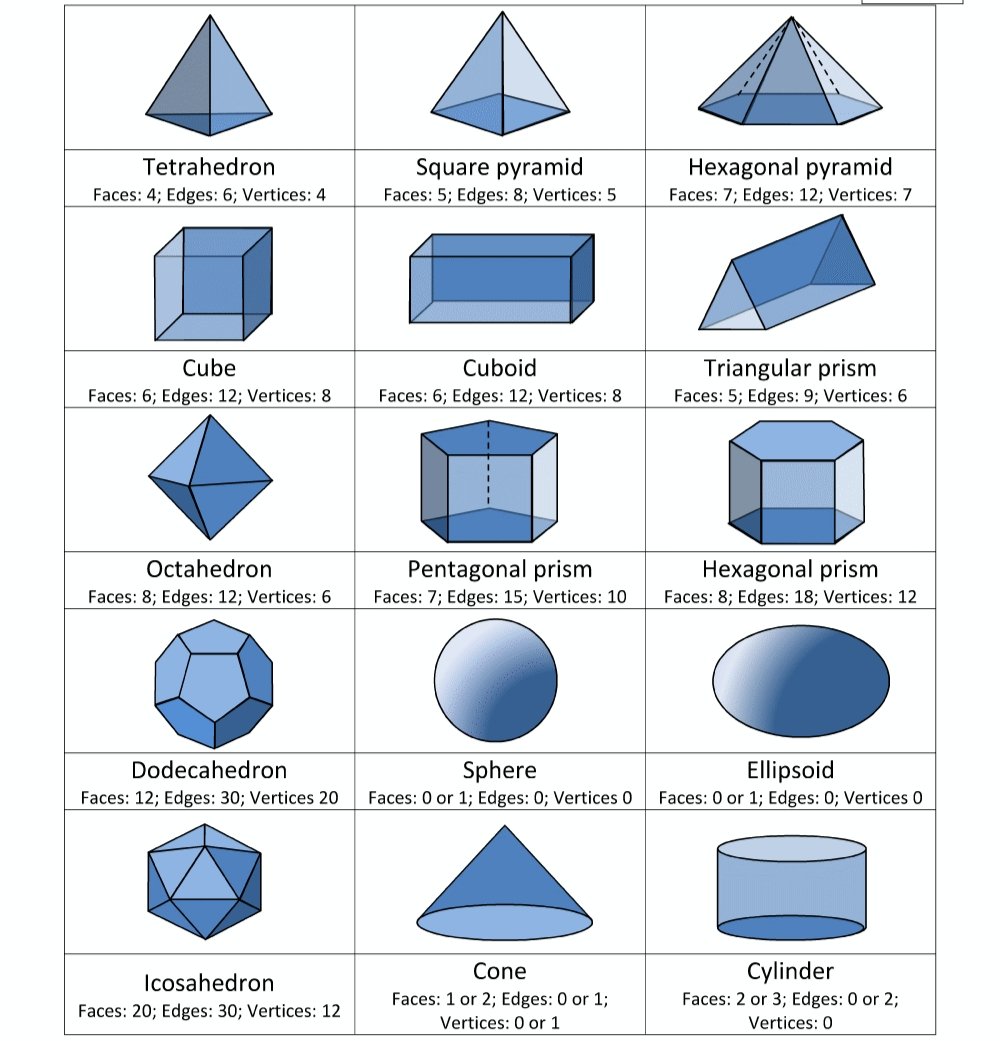
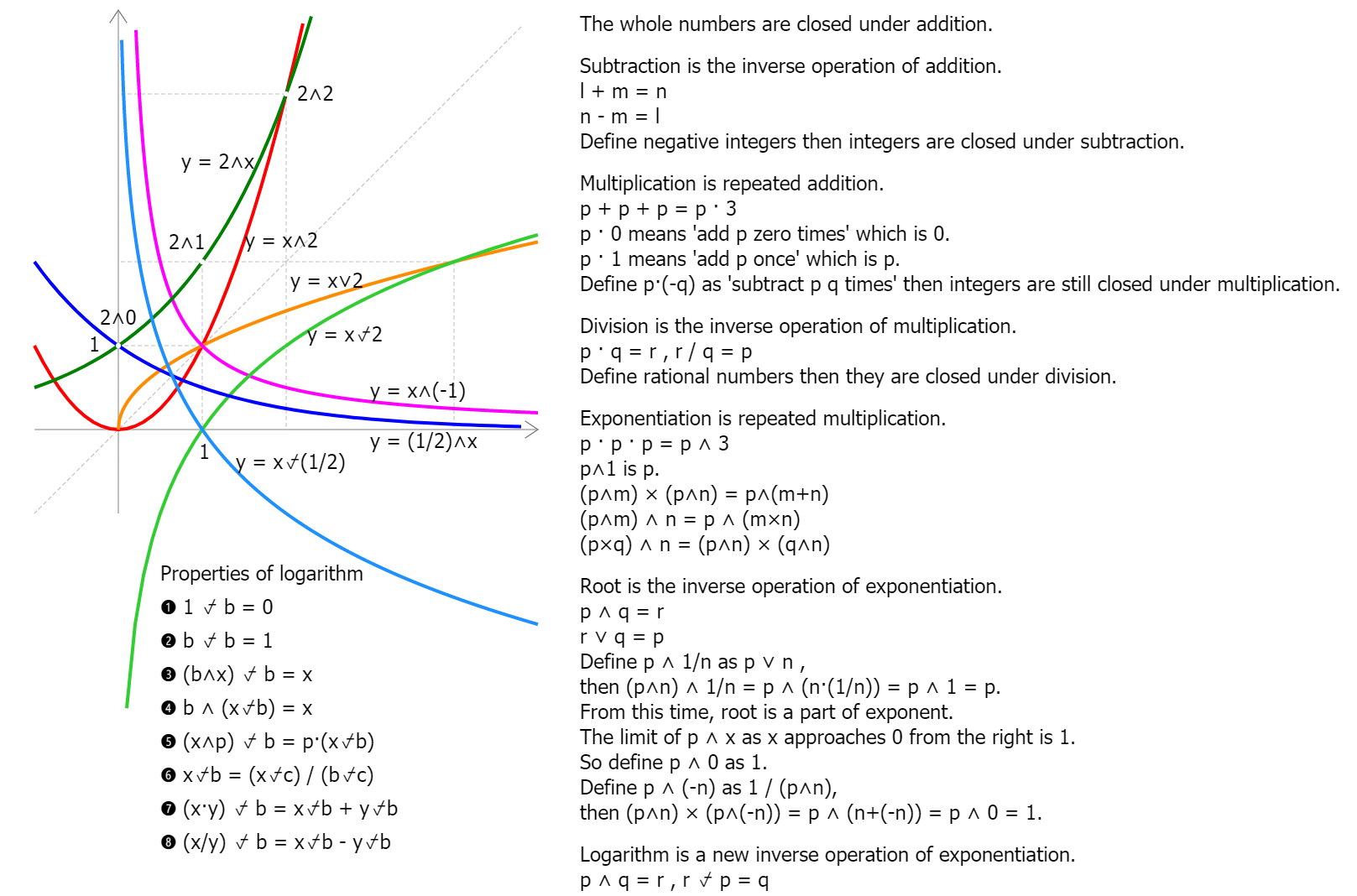
arithmetic, geometry, algebra, exponentiation, logarithm, trigonometry, calculus, topology
›
00 History
In mathematics, the notion of number has been extended over the centuries to include 0, negative numbers, rational numbers such as 1/2
and −2/3, real numbers such as √2 and π, and complex numbers, which extend the real numbers with √−1.
4758#5148
SIBLINGS
CHILDREN
OPEN







-











