math

EngliSea > M > math

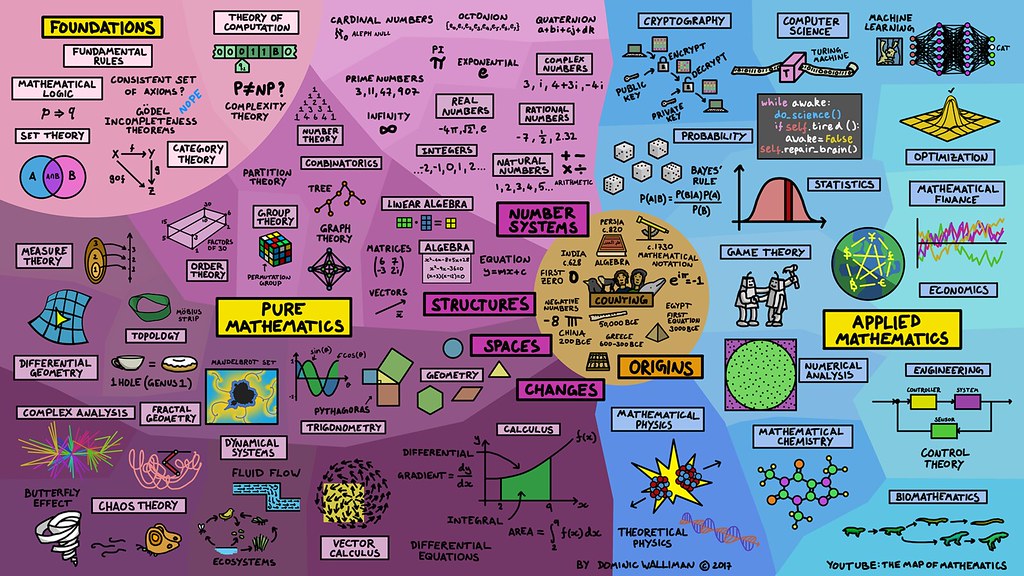
arithmetic, geometry, algebra, exponentiation, logarithm, trigonometry, calculus, topology

› litionary
4758#5079 SIBLINGS CHILDREN OPEN

• Map of Mathematics
4758#3676 SIBLINGS CHILDREN 3676

› 00 History
In mathematics, the notion of number has been extended over the centuries to include 0, negative numbers, rational numbers such as 1/2 and −2/3, real numbers such as √2 and π, and complex numbers, which extend the real numbers with √−1.
4758#5148 SIBLINGS CHILDREN OPEN

› 10 Arithmatic
The study of numbers, especially the properties of the traditional operations on them—addition, subtraction, multiplication and division.
4758#4816 SIBLINGS CHILDREN OPEN

• 15 2D shapes
4758#9553 SIBLINGS CHILDREN 9553

• 15 3D shapes
4758#9546 SIBLINGS CHILDREN 9546

› 15 Geometry
A branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space
4758#4999 SIBLINGS CHILDREN OPEN

• 20 Linear Equations
4758#9651 SIBLINGS CHILDREN 9651

• 20 Algebra properties
4758#9552 SIBLINGS CHILDREN 9552

› 20 Algebra
The study of mathematical symbols and the rules for manipulating these symbols
4758#4985 SIBLINGS CHILDREN OPEN

• 25 Exponent, root and logarithm
4758#3694 SIBLINGS CHILDREN COMMENT 3694

› 25 Exponent, root and logarithm
+plus (−minus) ↺ ·times (/over) ↺ ˄to (˅root ⍻log)
4758#5216 SIBLINGS CHILDREN OPEN

• 30 2 Dimensional Number
4758#9657 SIBLINGS CHILDREN 9657

› 30 Complex Number
The set C of complex numbers is the set R2 of ordered pairs of real numbers. a+bi = [a,b]
4758#9605 SIBLINGS CHILDREN OPEN

› 31 Vector
The Addition of 2 Dimensional Number ┆ 01 Introduction to Vectors and Their Operations ┆ 02 The Vector Dot Product ┆ Force Table ┆ Lever ┆ Vector

• 35 Linear Algebra
4758#3678 SIBLINGS CHILDREN COMMENT 3678

› 35 Linear Algebra
The branch of mathematics concerning linear equations, linear maps and their representations in vector spaces and through matrices.
4758#5093 SIBLINGS CHILDREN OPEN

› 40 Abstract Algebra
Set Theory

• 50 Trigonometric laws and identities
4758#3855 SIBLINGS CHILDREN 3855

› 50 Trigonometry
A branch of mathematics that studies relationships between side lengths and angles of triangles
4758#5019 SIBLINGS CHILDREN OPEN

› 55 Analysis
Fundamentals of Mathematical Analysis
4758#9702 SIBLINGS CHILDREN OPEN

• 60 Calculus - derivatives and limits
4758#3731 SIBLINGS CHILDREN 3731

• 60 Calculus - integrals
4758#3698 SIBLINGS CHILDREN 3698

› 60 Calculus
Whether differential or integral both concepts involve the idea that we can do something infinately many times and get a finite answer that is useful.
4758#5028 SIBLINGS CHILDREN OPEN

› 61 Multivariable Caculus

› 70 Topology
The mathematical study of the properties that are preserved through deformations, twistings, and stretchings of objects
4758#5233 SIBLINGS CHILDREN OPEN

› imaginary number
4758#23529 SIBLINGS CHILDREN OPEN

› New Notation
4758#32254 SIBLINGS CHILDREN OPEN

› tutorials
4758#28764 SIBLINGS CHILDREN OPEN

› ￤references
4758#9625 SIBLINGS CHILDREN OPEN