|
|
EngliSea > M > math > 25 Exponent, root and logarithm |
 •
05 Exponents In Algebra
•
05 Exponents In Algebra
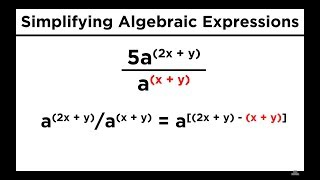 •
08 Simplifying Expressions With Roots and Exponents
•
08 Simplifying Expressions With Roots and Exponents
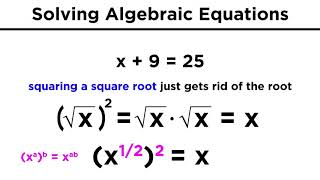 •
09 Solving Algebraic Equations With Roots and Exponents
•
09 Solving Algebraic Equations With Roots and Exponents
 •
41 Logarithms Part 1
•
41 Logarithms Part 1
 •
42 Logarithms Part 2
•
42 Logarithms Part 2
 •
43 Logarithms Part 3
•
43 Logarithms Part 3
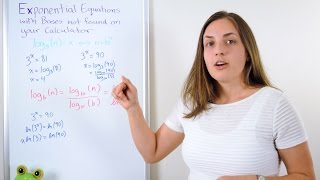 •
Change of base
•
Change of base
 •
exponential function
•
exponential function
 ◌◌◌
Exponentiation
◌◌◌
Exponentiation
 ◌◌◌
Logarithm
◌◌◌
Logarithm
 •
Logarithms Explained
•
Logarithms Explained